4. Hukum Kirchhoff
4.1. Hukum Kirchhoff pertama (hukum titik simpul)
Pada rangkaian parallel selalu menghasilkan apa yang disebut dengan titik percabangan, yang juga dikenal sebagai titik simpul.
Pada titik tersebut arusnya bercabang. Dalam hal ini sesuai dengan aturan tertentu.
Contoh:
Kita amati misalnya pada titik A beberapa arus sebagaimana diperlihatkan, maka ditemukan bahwa arus I1 dan I2 mengalir masuk menuju titik simpul A, sedangkan arus I3, I4 dan I5 mengalir keluar (meninggalkannya). Disini terbukti bahwa nilai arus yang masuk besarnya sama dengan nilai arus yang keluar.
Hukum Kirchhoff pertama (titik simpul):
Disetiap titik simpul (cabang), jumlah arus yang masuk besarnya sama dengan jumlah arus yang keluar.
I1 + I2 = I3 + I4 + I5
Dengan bantuan rumus ini, maka arus yang belum diketahui pada suatu titik percabangan arus, dapat ditentukan besarnya.
Contoh:
Berapa besarnya arus I2 pada rangkaian dibawah ini ?
Jawab: I = I1 + I2 + I3 dijabarkan ke I2 menjadi;
I2 = I - I1 - I3 ; I2 = 12 A - 5 A - 4 A = 3 A
4.2. Hukum Kirchhoff kedua (hukum jala-jala)
Pada suatu rangkaian arus tertutup (jala-jala) terdapat suatu pembagian tegangan yang sangat tertentu. Pembagian tegangan tersebut dapat dihitung dengan menggunakan rumus yang sesuai.
Contoh:
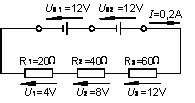
Kedua sumber tegangan dengan tegangan sumber US1 dan US2 elektron-elektronnya menggabungkan diri dalam memberikan pengaruhnya secara keseluruhan. Disini sumber tegangan tersebut bereaksi dalam arah yang sama. Mereka mengendalikan arus I sesuai dengan tahanan yang ada.
Pada suatu persamaan antara tegangan sumber dengan tegangan jatuh diketahui, bahwa hal tersebut sama besarnya, artinya yaitu tegangan sumber terbagi kedalam rangkaian arus secara keseluruhan.
Dari situ dapat disimpulkan hukum Kirchhoff kedua (hukum jala-jala):
Disetiap rangkaian arus tertutup, jumlah tegangan sumber besarnya sama dengan jumlah semua tegangan jatuh.
US1 + US2 = I . R1 + I . R2 + I . R3
Dalam praktiknya suatu rangkaian arus biasanya hanya terdiri atas sebuah tegangan sumber dan satu atau beberapa beban.
Disini berlaku:
US = I . R1 + I . R2
Kita hubungkan lampu seperti yang tersebut diatas pada suatu kotak kontak, dengan demikian maka tegangan klem U kotak kontak dalam hal ini berfungsi sebagai tegangan sumber US.
Maka berlaku:
U = I . R1 + I . R2; disederhanakan menjadi: U = I (R1 + R2)
Hukum Kirchhoff kedua (hukum jala-jala) dapat digunakan untuk bermacam-macam. Dia memungkinkan untuk menentukan suatu tegangan sumber yang belum diketahui, arus atau suatu tahanan.
Contoh:
Berapa besarnya nilai arus yang ditunjukkan amperemeter pada rangkaian dibawah ini ?
US1 + US2 + US3 = I . R1 + I . R2
US1 + US2 + US3 = I . (R1 + R2)
Jawaban:
Tegangan sumber semuanya berpengaruh dengan arah yang sama, pengaruhnya saling menggabungkan diri. Maka berlaku hukum Kirchhoff kedua (hukum jala-jala) :